Treści programowe
Wykłady
- Podstawowe typy architektur i pojęcia z nimi związane.
- Problemy w implementacji architektury potokowej i superskalarnej; metody ich rozwiązywania i wynikające z nich podukłady mikroprocesorów.
- Charakterystyka architektury wybranych współczesnych procesorów wykorzystywanych w urządzeniach stacjonarnych, mobilnych oraz superkomputerach.
- Komunikacja pomiędzy procesorem, pamięcią a urządzeniami wejścia/wyjścia.
- Charakterystyka architektury wybranych komputerów stacjonarnych oraz urządzeń mobilnych.
- Współczesne pamięci operacyjne / podstawowe parametry statyczne i dynamiczne.
- Typy magistral i ich parametry.
- Benchmarki.
- Charakterystyka mikrokomputerów jednoukładowych i ich przeznaczenie.
Ćwiczenia
Analiza szybkości wykonywania operacji stało- i zmiennoprzecinkowych.
Analiza cyklu rozkazowego i potoku rozkazowego w jednym rdzeniu procesora jedno i wielordzeniowego.
Komunikacja z pamięcią oraz z urządzeniami wejścia/wyjścia oraz obsługa przerwań.
Analiza działania wybranych instrukcji i przykładowych programów w asemblerze wybranego procesora.
Tworzenie przykładowych programów w asemblerze z wykorzystaniem instrukcji warunkowych i pętli.
Oprogramowanie układu sterującego dla przykładowego zadania (np. sterowanie światłami na skrzyżowaniu, obsługą żądań przywołania windy itp.).
Organizacja
- Jeśli ktoś jest zainteresowany, proponuję włączyć kamerę - na tej podstawie sprawdzam obecność
- Aktywność generuje plusy
- Wyniki, rezultaty z ćwiczeń proszę wklejać na czat
- Zaliczenie przedmiotu - kolokwium lub projekt
- Jeśli kolokwium to odbędzie się na przedostatnich zajęciach (zakres ściśle powiązany ze skryptem)
- Jeśli projekt, to prezentacja na ostatnich zajęciach - najprawdopodobniej stworzenie symulatora, powiązanego z tematyką zajęć.
- Zajęcia mają formułę warsztatów
- Trochę omawiamy temat
- Przeklejamy przykładowe programy lub programujemy je
- W dowolnym momencie proszę pytać o cokolwiek co jest związane z tematyką zajęć
Wstęp
Kilka problemów związanych z architekturą procesora i organizacją systemu komputerowego:
Reordering instrukcji: Procesory mogą zmieniać kolejność wykonywania instrukcji, aby zoptymalizować wydajność. Może to prowadzić do problemów związanych z synchronizacją wątków i niezdefiniowanym zachowaniem. Aby temu zapobiec, można użyć odpowiednich metod synchronizacji, takich jak muteksy, blokady czy bariery pamięci.
Efekty związane z pamięcią cache: Dostęp do pamięci ma istotny wpływ na wydajność programu. Wysokiej wydajności algorytmy powinny być zaprojektowane z uwzględnieniem hierarchii pamięci, tak aby minimalizować opóźnienia związane z odwołaniami do pamięci. Można to osiągnąć, stosując techniki optymalizacji, takie jak blokowanie, użycie pamięci lokalnej czy cache-oblivious algorithms.
Równoczesność i współbieżność: Wykorzystanie wielowątkowości i wielordzeniowości procesorów może prowadzić do problemów związanych z dostępem do wspólnych zasobów, takich jak dane czy urządzenia wejścia/wyjścia. Aby zapewnić poprawną współpracę wątków, można stosować mechanizmy synchronizacji (muteksy, semafory, blokady) oraz techniki programowania równoległego, takie jak zadania, przetwarzanie równoległe czy potoki.
Wydajność arytmetyki zmiennoprzecinkowej: Obliczenia zmiennoprzecinkowe różnią się wydajnością w zależności od architektury procesora. Aby uzyskać najlepszą wydajność, można stosować optymalizacje specyficzne dla danego procesora, takie jak wektoryzacja, instrukcje SIMD czy optymalizacja obliczeń matematycznych.
Obsługa błędów sprzętowych: Błędy sprzętowe, takie jak błędy parzystości czy uszkodzenia pamięci, mogą wpłynąć na poprawność działania programu. Można zastosować techniki wykrywania i naprawy błędów, takie jak korekcja błędów pamięci czy sprawdzanie parzystości, aby zminimalizować ryzyko wprowadzenia błędów przez sprzęt.
Aby uniknąć tych problemów i zapewnić poprawne działanie programu, ważne jest zapoznanie się z architekturą procesora, na którym ma być uruchomiony program, oraz zastosowanie odpowiednich technik programowania i optymalizacji. Oto kilka dodatkowych wskazówek:
Endianness: Kolejność bajtów w reprezentacji liczb wielobajtowych (little-endian lub big-endian) różni się między różnymi architekturami procesorów.
Wydajność operacji wejścia/wyjścia: Operacje wejścia/wyjścia mają znaczący wpływ na wydajność aplikacji. W przypadku programów wymagających intensywnego przepływu danych, należy zastosować techniki buforowania, asynchronicznych operacji wejścia/wyjścia oraz optymalizować użycie systemów plików i urządzeń wejścia/wyjścia.
Granice stronicowania: Dostęp do pamięci może być niejednorodny z powodu granic stronicowania. Aby uniknąć opóźnień związanych z przenoszeniem danych między stronami pamięci, można zastosować techniki takie jak wyrównywanie stronicowania (page alignment), stosowanie dużych stron (huge pages) czy ograniczenie fragmentacji pamięci.
Architektura NUMA (Non-Uniform Memory Access): W przypadku systemów wieloprocesorowych z architekturą NUMA, dostęp do pamięci może być wolniejszy dla niektórych rdzeni procesora. Aby zoptymalizować wydajność programów na takich systemach, można stosować techniki takie jak lokalność danych, afinitet rdzeni czy specjalne funkcje alokacji pamięci, takie jak
numa_alloc_onnodeinuma_bind.Wsparcie dla instrukcji specyficznych dla procesora: Niektóre procesory mają instrukcje, które pozwalają na bardziej efektywne wykonanie określonych operacji. Można skorzystać z tych instrukcji, pisząc kod w asemblerze lub korzystając z bibliotek, które wykorzystują te instrukcje, takie jak biblioteki matematyczne czy algorytmiczne.
Aby uniknąć problemów związanych z architekturą procesora i organizacją systemu komputerowego, ważne jest, aby programować z uwzględnieniem tych zagadnień. Dobrym podejściem jest też korzystanie z bibliotek i narzędzi, które już zostały zoptymalizowane pod kątem różnych architektur i systemów.
Ref:
- Architektura systoliczna - np. Edge TPU
- Google Coral Edge TPU explained in depth
- Cell (PS3) - PowerPC (PPE) + 7 x „Synergistic Processing Elements” (SPEs) PlayStation 3
- Hardware for Deep Learning
- Unlocking the Secrets of GPU Architecture
- A CPU is a compiler
Reprezentacja liczb
System dziesiętny
Liczba 13910 jest zapisana w systemie dziesiętnym, co oznacza, że każda pozycja odpowiada potędze liczby 10. System pozycyjny to sposób zapisu liczb, w którym wartość liczby zależy od wartości cyfr i ich pozycji. W systemie wagowym wartość liczby jest sumą iloczynów cyfr i wag pozycji, gdzie wagi pozycji są potęgami podstawy systemu.
Liczba 13910 z rozbiciem na wagi poszczególnych pozycji:
1 * 10^4 +
3 * 10^3 +
9 * 10^2 +
1 * 10^1 +
0 * 10^0 =
10000 + 3000 + 900 + 10 + 0 = 13910
System binarny
Konwersja liczby 13910 na zapis binarny:
13910 : 2 = 6955 (reszta: 0)
6955 : 2 = 3477 (reszta: 1)
3477 : 2 = 1738 (reszta: 1)
1738 : 2 = 869 (reszta: 0)
869 : 2 = 434 (reszta: 1)
434 : 2 = 217 (reszta: 0)
217 : 2 = 108 (reszta: 1)
108 : 2 = 54 (reszta: 0)
54 : 2 = 27 (reszta: 0)
27 : 2 = 13 (reszta: 1)
13 : 2 = 6 (reszta: 1)
6 : 2 = 3 (reszta: 0)
3 : 2 = 1 (reszta: 1)
1 : 2 = 0 (reszta: 1)
Liczba binarna: 11 0110 0101 0110
Ćwiczenie
Zamienić na liczbę w notacji binarnej za pomocą powyższej metody:
- 19
- 1977
Naturalny kod binarny to sposób zapisu liczb, w którym wartość liczby jest sumą iloczynów cyfr i wag pozycji, gdzie wagi pozycji są potęgami liczby 2.
Liczba 1011 0101 z rozbiciem na wagi poszczególnych pozycji:
1 * 2^7 +
0 * 2^6 +
1 * 2^5 +
1 * 2^4 +
0 * 2^3 +
1 * 2^2 +
0 * 2^1 +
1 * 2^0 =
128 + 32 + 16 + 4 + 1 = 181
System szesnastkowy
| 0 | 0000 | 8 | 1000 |
| 1 | 0001 | 9 | 1001 |
| 2 | 0010 | A | 1010 |
| 3 | 0011 | B | 1011 |
| 4 | 0100 | C | 1100 |
| 5 | 0101 | D | 1101 |
| 6 | 0110 | E | 1110 |
| 7 | 0111 | F | 1111 |
Aby przekonwertować liczbę binarną 1011011100101101 na szesnastkowy, można ją podzielić na grupy po 4 bity i przypisać im wartości szesnastkowe:
1011 0111 0010 1101
B 7 2 D
Liczba szesnastkowa: B72D
Przechowywanie danych w komputerach
Narysować pamięć
Dane w komputerze są przechowywane w postaci binarnej, czyli za pomocą bitów (0 i 1). System binarny został wybrany ze względu na prostotę realizacji elektronicznej (wysokie i niskie napięcie) oraz łatwość przetwarzania informacji.
Rejestr to mały obszar pamięci w procesorze, używany do przechowywania wartości, które są obecnie przetwarzane. Słowo to ciąg bitów, który odpowiada długości rejestru lub jednostki przetwarzania danych.
Załóżmy, że mamy rejestr 8-bitowy. Aby zapisać wartość 139 (10001011) w rejestrze, wystarczy ustawić bity na odpowiednie wartości: 10001011
Ile bitów jest potrzebnych na zapisanie liczby 139, 255, 269, 513?
139: 8 bitów (10001011)
255: 8 bitów (11111111)
269: 9 bitów (100001101)
513: 10 bitów (1000000001)
Liczba potrzebnych bitów do zapisania każdej z tych liczb zależy od ich wartości w postaci binarnej. Aby określić minimalną ilość bitów potrzebną do zapisania danej liczby, można zastosować funkcję logarytmu dwójkowego (lub log2), a następnie zaokrąglić wynik w górę do najbliższej liczby całkowitej.
| |
Co to jest rejestr?
Nadmiar i niedomiar
Ćwiczenie
- Czy wynik operacji mieści się w 8-bitowym rejestrze? (nadmiar czy niedomiar)
- Ile bitów potrzeba do reprezentacji wyniku?
Dodawanie:
A = 127 (01111111) B = 4 (00000100) A + B = 131 (10000011)Dodawanie:
A = 139 (10001011) B = 147 (10010011) A + B = 286 (1 00010010) efekt nadmiaru, wynik nie mieści się w 8-bitowym rejestrze.
W drugim przypadku mamy do czynienia z nadmiarem, co oznacza, że wynik przekracza maksymalną wartość, która może być przechowywana w 8-bitowym rejestrze (255).
Odejmowanie:
A = 115 (01110011) B = 5 (00000101) C = A - B = 110 (01101110)Odejmowanie:
A = 129 (10000001) B = 167 (10100111) C = A - B = -38 (11011010) efekt niedomiaru, ponieważ wynik jest liczbą ujemną.
Liczby ujemne
- Z bitem znaku
- U2
Aby zapisać liczbę -2 w 8-bitowym rejestrze, używamy kodu U2 (Uzupełnienie do 2):
-2 = 11111110
Przykład dla liczby 10110101:
Jako liczba dodatnia:
1 * 2^7 + 0 * 2^6 + 1 * 2^5 + 1 * 2^4 + 0 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 128 + 32 + 16 + 4 + 1 = 181Jako liczba ujemna (w kodzie U2):
~1011 0101 + 1 = 0100 1010 + 1 = 0100 1011 co daje: 64 + 8 + 2 + 1 = 75, więc liczba to -75.
Interpretacja liczby zależy od kontekstu. W przypadku liczb ujemnych często stosowany jest kod U2.
Kod U2
Uzupełnienie do 2, to metoda reprezentacji liczb całkowitych, zarówno dodatnich, jak i ujemnych, w systemie binarnym. W kodzie U2 liczby dodatnie są reprezentowane tak samo jak w naturalnym kodzie binarnym, natomiast liczby ujemne są reprezentowane jako dopełnienie do 2 liczby bezwzględnej.
Obliczanie reprezentację liczby ujemnej w kodzie U2:
- Przekształć wartość bezwzględną liczby ujemnej na postać binarną.
- Odwróć bity (zmień 0 na 1 i 1 na 0).
- Dodaj 1 do wyniku.
Przykłady:
Przykład dla liczby -3:
1. Wartość bezwzględna: 3 (w binarnym: 0000 0011) 2. Odwrócenie bitów: 1111 1100 3. Dodanie 1: 1111 1100 + 1 = 1111 1101 Kod U2 dla liczby -3: 1111 1101Przykład dla liczby -7:
1. Wartość bezwzględna: 7 (w binarnym: 0000 0111) 2. Odwrócenie bitów: 1111 1000 3. Dodanie 1: 1111 1000 + 1 = 1111 1001 Kod U2 dla liczby -7: 1111 1001
Kod U2 jest często stosowany w komputerach, ponieważ pozwala na wykonywanie operacji dodawania i odejmowania przy użyciu tego samego sprzętu, niezależnie od znaku liczb.
Ćwiczenie
- -7
- -117
Liczby rzeczywiste
11 i 5/16 = 11.3125
Liczba 11 w postaci binarnej to 1011.
5/16 jako ułamek binarny to 0.0101 ponieważ
1 * (1/2)^3 +
0 * (1/2)^4 +
1 * (1/2)^5)
0.3125 * 2 = 0.625 -> 0
0.625 * 2 = 1.25 -> 1
0.25 * 2 = 0.5 -> 0
0.5 * 2 = 1 -> 1
Liczba 11 i 5/16 w postaci binarnej to: 1011.0101
Potrzebujemy 8 bitów na zapisanie tej liczby. Można zapisać ją w rejestrze jako liczba stałoprzecinkowa (zakładając, że przecinek jest zawsze pomiędzy bitami 3 i 4) lub używając notacji zmiennoprzecinkowej, która pozwala na zapisanie liczby z określoną precyzją i zakresem.
Zamiana na postać binarną
Aby przekształcić liczbę dziesiętną 10.75 na liczbę binarną, należy przekształcić osobno jej część całkowitą i część ułamkową.
Konwersja części całkowitej:
Liczba całkowita: 10 Postępujemy według metody dzielenia przez 2: 10 / 2 = 5, reszta: 0 5 / 2 = 2, reszta: 1 2 / 2 = 1, reszta: 0 1 / 2 = 0, reszta: 1 Czytamy reszty od dołu do góry: 1010Konwersja części ułamkowej:
Liczba ułamkowa: 0.75 Postępujemy według metody mnożenia przez 2: 0.75 * 2 = 1.5 (zapisujemy cyfrę 1) 0.50 * 2 = 1.0 (zapisujemy cyfrę 1) Czytam od góry do dołu: 11
Teraz, aby uzyskać postać binarną liczby 10.75, łączymy część całkowitą (1010) i część ułamkową (11) za pomocą przecinka binarnego: 1010.11
Stąd wynika, że liczba dziesiętna 10.75 jest równa liczbie binarnej 1010.11
Uwaga Podczas konwersji liczby ułamkowej dziesiętnej na liczbę binarną za pomocą metody mnożenia przez 2, należy zakończyć mnożenie w jednym z następujących przypadków:
Gdy wartość ułamkowa po mnożeniu wynosi dokładnie 0. Wtedy wszystkie kolejne mnożenia również będą dawały 0, a kolejne cyfry binarne po przecinku będą się składały wyłącznie z zer. W takiej sytuacji nie > ma potrzeby kontynuować obliczeń.
Gdy osiągniesz żądaną precyzję. W praktyce, liczby binarne używane w komputerach mają ograniczoną precyzję (np. w przypadku liczb zmiennoprzecinkowych w standardzie IEEE-754). W związku z tym możemy > zakończyć mnożenie po osiągnięciu określonej liczby cyfr binarnych po przecinku.
Gdy zauważysz cykliczne powtarzanie się wzoru cyfr. W niektórych przypadkach, liczby ułamkowe dziesiętne mają nieskończoną reprezentację binarną, która powtarza się cyklicznie. Kiedy zauważysz taki wzór, > możesz zakończyć mnożenie i zaokrąglić wynik do żądanej precyzji.
Należy pamiętać, że niektóre liczby ułamkowe dziesiętne mają nieskończoną reprezentację binarną, która nie wykazuje cyklicznego powtarzania się wzoru. W takich przypadkach, można zakończyć mnożenie, gdy > osiągnięta zostanie żądana precyzja, biorąc pod uwagę ograniczenia sprzętowe lub wymagania dotyczące zaokrąglenia.
Przykłady
Liczba dziesiętna 0.5:
0.5 * 2 = 1.0 (zapisujemy cyfrę 1) Binarnie: 0.1Liczba dziesiętna 0.25:
0.25 * 2 = 0.5 (zapisujemy cyfrę 0) 0.5 * 2 = 1.0 (zapisujemy cyfrę 1) Binarnie: 0.01Liczba dziesiętna 0.625:
0.625 * 2 = 1.25 (zapisujemy cyfrę 1) 0.25 * 2 = 0.5 (zapisujemy cyfrę 0) 0.5 * 2 = 1.0 (zapisujemy cyfrę 1) Binarnie: 0.101Liczba dziesiętna 0.375:
0.375 * 2 = 0.75 (zapisujemy cyfrę 0) 0.75 * 2 = 1.5 (zapisujemy cyfrę 1) 0.5 * 2 = 1.0 (zapisujemy cyfrę 1) Binarnie: 0.011Liczba dziesiętna 0.1977:
0.1977 * 2 = 0.3954 -> (0.0) 0.3954 * 2 = 0.7908 -> (0.00) 0.7908 * 2 = 1.5816 -> (0.001) 0.5816 * 2 = 1.1632 -> (0.0011) 0.1632 * 2 = 0.3264 -> (0.00110) 0.3264 * 2 = 0.6528 -> (0.001100) 0.6528 * 2 = 1.3056 -> (0.0011001)
Warto zauważyć, że niektóre liczby ułamkowe w systemie dziesiętnym nie mają dokładnej reprezentacji w systemie binarnym.
Liczba dziesiętna 0.1:
0.1 * 2 = 0.2 (zapisujemy cyfrę 0) 0.2 * 2 = 0.4 (zapisujemy cyfrę 0) 0.4 * 2 = 0.8 (zapisujemy cyfrę 0) 0.8 * 2 = 1.6 (zapisujemy cyfrę 1) 0.6 * 2 = 1.2 (zapisujemy cyfrę 1) 0.2 * 2 = 0.4 (zapisujemy cyfrę 0) ... Binarnie: 0.0001100110011... (cyfry się powtarzają)
W takich przypadkach reprezentacja binarna będzie nieskończoną liczbą cyfr po przecinku i musi zostać zaokrąglona, aby zmieścić się w określonym formacie, takim jak standard IEEE-754.
Notacja zmiennoprzecinkowa
W komputerach najczęściej stosowaną notacją zmiennoprzecinkową jest standard IEEE-754. Standard ten definiuje formaty reprezentacji liczb zmiennoprzecinkowych, takie jak pojedyncza precyzja (32 bity) i podwójna precyzja (64 bity). Standard IEEE-754 pozwala na zapisanie liczb z określoną precyzją, zakresem i specjalnymi wartościami (takimi jak nieskończoność i NaN). Na niektórych platformach dostępny jest typ half-float (NVidia CUDA) o połowicznej precyzji (16 bitów)
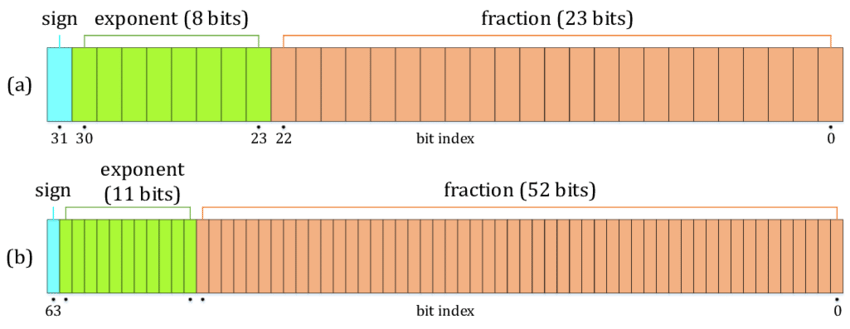
Reprezentacja liczby zmiennoprzecinkowej w standardzie IEEE-754 składa się z trzech części:
- Znak (Sign) - jeden bit, który reprezentuje znak liczby (0 - dodatnia, 1 - ujemna).
- Wykładnik (Exponent) - ciąg bitów reprezentujący wykładnik liczby, przesunięty o wartość stałą (bias). Dla formatu pojedynczej precyzji przesunięcie wynosi 127, a dla podwójnej precyzji wynosi 1023.
- Mantysa (Significand) - ciąg bitów reprezentujący wartość liczby znormalizowanej, ale bez pierwszego bitu (1), który jest zawsze niejawny (chyba że liczba jest denormalizowana).
Tworzenie reprezentacji binarnej liczby zmiennoprzecinkowej w standardzie IEEE-754:
- Określ znak liczby (0 dla dodatniej, 1 dla ujemnej).
- Zamienić część dziesiętną oraz ułamkową na postać binarną.
- Przekształć liczbę na postać znormalizowaną w notacji naukowej (1.x * 2^n).
- Oblicz wykładnik, dodając przesunięcie (bias) do n (wykładnik notacji naukowej).
- Przekształć mantysę na postać binarną, pomijając pierwszy bit (1).
- Złożyć reprezentację z części znakowej, wykładnika i mantysy.
Przykład:
Chcemy zapisać liczbę 10.75 jako liczbę zmiennoprzecinkową w standardzie IEEE-754 (pojedyncza precyzja).
- Liczba jest dodatnia, więc znak to 0.
- Postać binarną: 10.75 = 1010.11
- Postać znormalizowana: 1.01011 * 2^3
- Wykładnik: 3 + 127 (bias) = 130, w postaci binarnej: 10000010
- Mantysa (bez pierwszego bitu): 0101100… (w sumie 23 bity)
- Składamy reprezentację: 0 10000010 01011000000000000000000
Reprezentacja liczby 10.75 w standardzie IEEE-754 (pojedyncza precyzja) to:
32 31 30 29 28 27 26 25 24 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1
0 1 0 0 0 0 0 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
1 * 2^3 * 1.34375 = 10.75
Ref:
Kolejność bajtów
Przykład reprezentacji liczby 32-bitowej (4-bajtowej) w różnych kolejnościach bajtów:
Wartość: 0x12345678
- Little-endian: 78 56 34 12
- Big-endian: 12 34 56 78
Poniżej znajduje się przykładowy program w C++, który demonstruje różne kolejności bajtów:
Lab_01:
| |
Różne procesory używają różnych kolejności bajtów:
- Little-endian: Procesory Intel x86, x86-64 oraz większość mikrokontrolerów ARM (w trybie little-endian).
- Big-endian: Procesory Motorola 68k, PowerPC, IBM z/Architecture, a także niektóre mikrokontrolery ARM (w trybie big-endian).
Wybór kolejności bajtów jest często wynikiem decyzji projektowych, które miały na celu ułatwienie lub optymalizację wykonywania określonych operacji. Little-endian jest popularne ze względu na prostotę dodawania i odejmowania liczb o zmiennej długości oraz łatwiejszą obsługę liczb o mniejszej precyzji w reprezentacji o większej precyzji. Big-endian jest częściej stosowany w systemach, które muszą współpracować z sieciami komputerowymi, gdzie bajty są przesyłane od najbardziej znaczącego do najmniej znaczącego, co ułatwia interpretację wartości przesyłanych danych.
Ref:
Wykonywania operacji stało- i zmiennoprzecinkowych:
FPU (Floating Point Unit) to podzespoły procesora odpowiedzialne za wykonywanie operacji arytmetycznych na liczbach zmiennoprzecinkowych. Liczba jednostek FPU może się różnić w zależności od architektury i modelu procesora. Oto kilka przykładów:
- Intel Core i7-8700K (8. generacja Core)
- 6 rdzeni, każdy z jednostką FPU - 6 jednostek FPU.
- AMD Ryzen 7 3700X (3. generacja Ryzen)
- 8 rdzeni, każdy z jednostką FPU - 8 jednostek FPU.
- Apple M1 (ARM-based)
- 8 rdzeni CPU (4 wysokiej wydajności i 4 energooszczędne), każdy z jednostką FPU - 8 jednostek FPU.
- IBM POWER9
- 12 lub 24 rdzenie, w zależności od konfiguracji. Każdy rdzeń ma jedną jednostkę FPU - 12 lub 24 jednostki FPU.
- NVIDIA A100 (GPU)
- W przypadku GPU, jednostki FPU są zintegrowane z procesorami strumieniowymi (CUDA cores). NVIDIA A100 posiada 6912 rdzeni CUDA.
Warto zauważyć, że w przypadku GPU, jednostki FPU mogą być wykorzystywane do obliczeń równoległych, ale zwykle nie są one traktowane jako oddzielne jednostki, tak jak w przypadku CPU.
Porównanie czasu wykonywania
Porównanie czasu wykonywania dodawania, odejmowania, mnożenia i dzielenia dla liczby stałoprzecinkowej (int) i zmiennoprzecinkowej (float, double).
- Utwórz program, który generuje losowe liczby int oraz float (lub double) i wykonuje podstawowe operacje matematyczne.
- Zmierz czas wykonania każdej operacji dla różnych precyzji.
- Porównaj wyniki i zastanów się nad wpływem precyzji na czas wykonania operacji.
Lab_02:
| |
Ten program w C++ analizuje wpływ precyzji zmiennoprzecinkowej na czas wykonania operacji. Wykonuje on podstawowe operacje matematyczne (+, -, *, /) na liczbach całkowitychoraz zmiennoprzecinkowych o różnych precyzjach (float, double) i mierzy czas wykonania tych operacji za pomocą biblioteki <chrono>.
Po skompilowaniu i uruchomieniu programu, na konsoli zostaną wyświetlone wyniki czasu wykonania operacji dla różnych precyzji. Należy przeanalizować wyniki i zastanowić się nad wpływem precyzji na czas wykonania operacji.
Obliczanie czasu wykonywania operacji na macierzach stało- i zmiennoprzecinkowych.
- Napisz program, który mnoży dwie macierze o ustalonych rozmiarach, używając typów stałoprzecinkowych (int) oraz zmiennoprzecinkowych (float, double).
- Zmierz czas wykonania mnożenia macierzy dla różnych rozmiarów macierzy.
- Porównaj wyniki i omów znaczenie różnic w czasie wykonania dla różnych typów danych.
Lab_04:
| |
Program mnoży dwie macierze o ustalonych rozmiarach, używając typów stałoprzecinkowych (int) oraz zmiennoprzecinkowych (float, double). Następnie, mierzy czas wykonania mnożenia macierzy dla różnych rozmiarów macierzy (100x100, 500x500, 1000x1000) i porównuje wyniki dla różnych typów danych.
Po skompilowaniu i uruchomieniu programu, na konsoli zostaną wyświetlone wyniki czasu wykonania mnożenia macierzy dla różnych rozmiarów macierzy i typów danych. Porównaj wyniki i omów znaczenie różnic w czasie wykonania dla różnych typów danych.
Wyniki mogą się różnić w zależności od sprzętu i kompilatora. Analizuj różnice między typami danych (stałoprzecinkowe i zmiennoprzecinkowe) oraz rozmiarami macierzy. Zwróć uwagę na to, jak zmienia się czas wykonania w zależności od typu danych i rozmiaru macierzy. Zastanów się, jak te różnice wpływają na wydajność w praktycznych zastosowaniach, takich jak obliczenia naukowe, analiza danych czy grafika komputerowa.
W praktyce, wybór między typami danych zależy od wymagań dotyczących precyzji, wydajności i dostępnych zasobów. W przypadku obliczeń naukowych i analizy danych, precyzja może być kluczowa, ale jednocześnie może wpłynąć na czas wykonania. W grafice komputerowej, mniejsza precyzja może być akceptowalna, ale szybsze obliczenia mogą być kluczowe dla płynności działania aplikacji.
Eksperyment z optymalizacją kodu.
- Napisz prosty program, który wykonuje operacje matematyczne na liczbach stało- i zmiennoprzecinkowych.
- Skompiluj i uruchom program z różnymi poziomami optymalizacji (np. -O0, -O1, -O2, -O3).
- Porównaj czas wykonania programu dla różnych poziomów optymalizacji i zastanów się, jak optymalizacja wpływa na wydajność operacji stało- i zmiennoprzecinkowych.
Wprowadzenie do instrukcji SIMD.
- Zapoznaj się z instrukcjami SIMD (Single Instruction, Multiple Data) dostępnymi dla Twojego procesora (np. SSE, AVX).
- Napisz program, który wykonuje operacje matematyczne na wektorach liczb stało- i zmiennoprzecinkowych, wykorzystując instrukcje SIMD.
- Porównaj czas wykonania operacji wektorowych z użyciem SIMD do czasu wykonania operacji
Aby użyć instrukcji SIMD w C++, możemy wykorzystać bibliotekę immintrin.h, która obsługuje instrukcje SSE, SSE2, SSE3, SSSE3, SSE4.1, SSE4.2, AVX, AVX2 i AVX-512.
Poniżej znajduje się przykład programu w C++, który wykonuje operacje dodawania na wektorach liczb stało- i zmiennoprzecinkowych, wykorzystując instrukcje SIMD. Porównuje czas wykonania operacji wektorowych z użyciem SIMD do czasu wykonania operacji bez SIMD.
| |
W tym przypadku, używamy instrukcji SIMD dla operacji dodawania wektorów zmiennoprzecinkowych (float). Program porównuje czas wykonania operacji wektorowych z użyciem SIMD do czasu wykonania operacji bez SIMD dla typów int, float i double. Po skompilowaniu i uruchomieniu programu, na konsoli zostaną wyświetlone wyniki czasu wykonania dodawania wektorów dla różnych typów danych, zarówno z użyciem SIMD, jak i bez.
Wyniki mogą się różnić w zależności od sprzętu i kompilatora, ale zazwyczaj SIMD przyspiesza obliczenia wektorowe, gdyż pozwala na wykonywanie operacji na wielu elementach danych jednocześnie.
W praktyce, wykorzystanie SIMD może prowadzić do znacznego przyspieszenia obliczeń wektorowych, szczególnie w zastosowaniach, takich jak grafika komputerowa, analiza danych czy przetwarzanie sygnałów. Jednak warto pamiętać, że nie wszystkie operacje mogą być przyspieszone przy użyciu SIMD, a także, że optymalizacja przy użyciu SIMD może zwiększyć złożoność kodu i utrudnić jego utrzymanie.
Ref:
Porównawczy kod w asemblerze
Poniżej znajduje się przykład programu napisanego w asemblerze x86, który porównuje czas wykonania operacji dodawania, odejmowania, mnożenia i dzielenia dla liczby stałoprzecinkowej (int) i zmiennoprzecinkowej (float, double). Program korzysta z polecenia RDTSC do mierzenia czasu wykonania operacji.
| |
Aby skompilować i uruchomić program, można użyć narzędzi NASM i LD lub fasm
Należy pamiętać, że ten program nie wypisuje wyników na ekran, ale przechowuje je w zarezerwowanych zmiennych int_duration i float_duration. Aby wyświetlić wyniki, można dodać kod odpowiedzialny za wypisanie wartości na ekran, korzystając z systemu wywołań (syscalls) lub użyć debuggera, aby przejrzeć wartości tych zmiennych
Ref:
Architektura von Neumana
Architektura komputerów Von-Neumanna, zaproponowana przez Johna von Neumanna, opiera się na koncepcji przechowywania programów w pamięci komputera. Wcześniej, maszyny liczące były projektowane tak, aby wykonywać jedno konkretne zadanie i nie można było ich przeprogramować. Architektura von Neumanna wprowadziła założenie, że programy i dane mogą być przechowywane w tej samej pamięci, co umożliwiło rozwój maszyn uniwersalnych, które mogą wykonywać różne zadania.
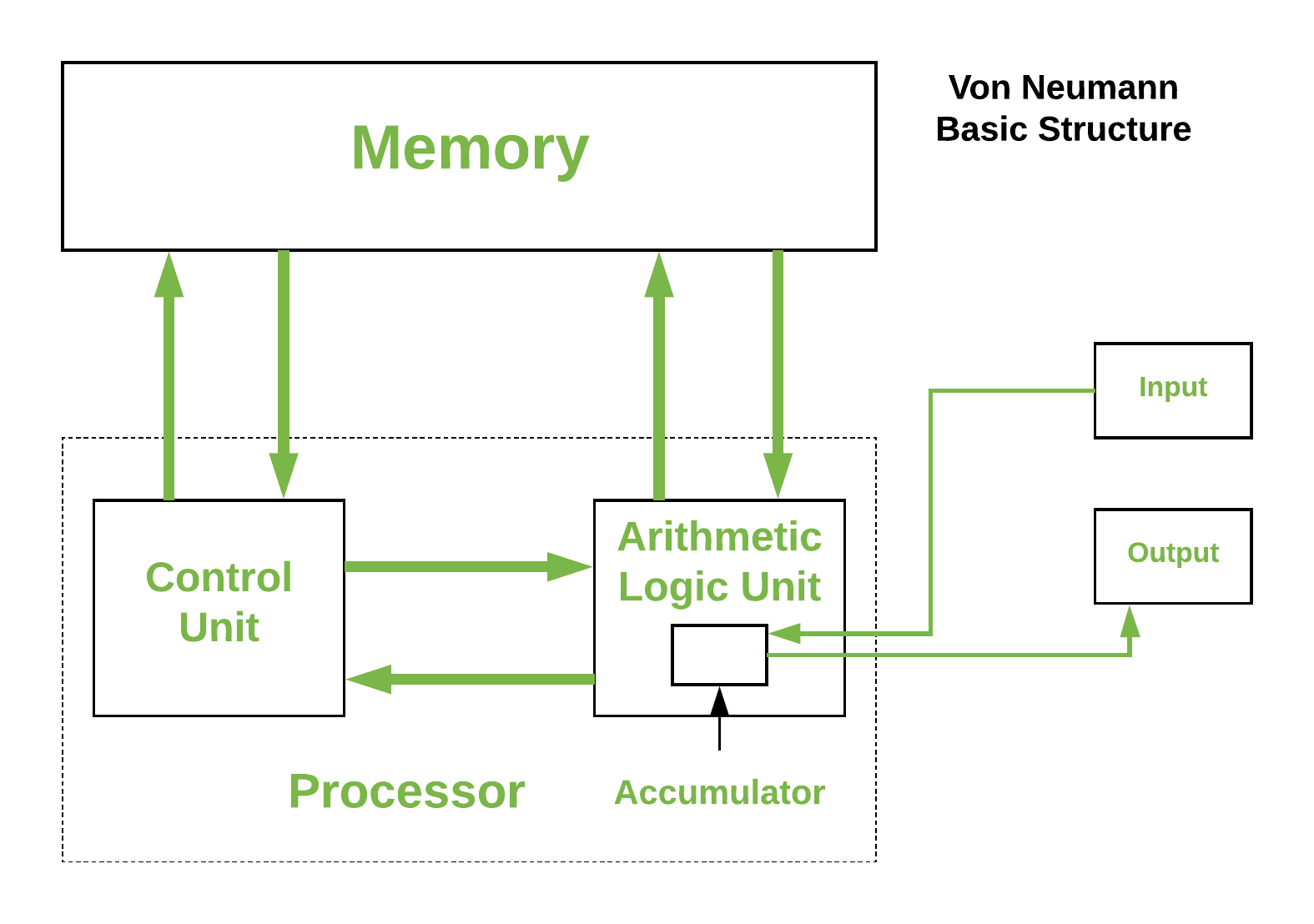
Podstawowe elementy architektury von Neumanna obejmują:
Pamięć: Służy do przechowywania danych i programów. Pamięć może być podzielona na dwie części: pamięć operacyjną (RAM) i pamięć trwałą (np. dysk twardy).
Procesor: Składa się z jednostki arytmetyczno-logicznej (ALU) oraz jednostki sterującej. ALU wykonuje operacje arytmetyczne i logiczne na danych, podczas gdy jednostka sterująca zarządza sekwencją operacji, odczytuje instrukcje z pamięci i decyduje, jakie operacje mają zostać wykonane.
Wejście/wyjście (I/O): Odpowiada za komunikację z urządzeniami zewnętrznymi, takimi jak klawiatura, mysz, monitor, drukarka itp.
System komunikacji: Składa się z szyny danych, szyny adresowej i szyny kontrolnej, które łączą poszczególne elementy komputera i umożliwiają wymianę informacji między nimi.
Architektura komputerów Von-Neumanna jest podstawą dla większości współczesnych komputerów i urządzeń, takich jak komputery osobiste, laptopy, serwery czy smartfony. Wraz z postępem technologicznym i rozwojem układów scalonych oraz mikroprocesorów, architektura von Neumanna została udoskonalona i przekształcona, ale jej podstawowe zasady wciąż pozostają aktualne.
ISA (Instruction set architecture) i posiada trzy podstawowe jednostki:
- Centralna Jednostka Przetwarzająca (CPU)
- Control Unit(CU)
- Jednostka arytmetyczna i logiczna (ALU)
- Rejestry
- Jednostka pamięci głównej
- Urządzenie wejścia/wyjścia
Przykładowa symulacja architektury
| |
Przykład Lab_31.py
Instrukcje symulatora
Procesor posiada tylko jeden rejestr, akumulator A. Możliwe jest adresowanie bezpośrednie i pośrednie. Załóżmy, że akumulator jest 32bitowy.
- HLT - Zatrzymanie pracy
- LDA <> - Załadowanie do A danych z adresu
- STA - Wpisanie pod zadany adres w argumencie, wartości z rejestru A
- LDI - Załadowanie do A danych z adresu wskzanego pod podanym adresem
- INP - Załadowanie danych do A z urządzenia we/wy
- OUT - Wysłanie wartości A na wyjście
- ADD - Dodanie wartości z pamięci wskazanej przez argument do A
- SUB - Odjęcie od A wartości z pamięci wskazanej przez argument
- CMP - Porównanie A z wartoścą pamięci wskazanej przez argument, wynik w A 0 jesli równe, 1 jeśli różne
- MOV - Wpisanie do A bezpośredniej wartości
- INC - Zwiększenie A o jeden
- DEC - Zmniejszenie A o jeden
- JMP - Skok bezwarunkowy
- JZ - Skok jeśli A jest równe zero
Składnia assemblera:
:etykieta - etykieta, wskazująca na miejsce w pamięci
@etykieta - poinformowanie kompilator, aby zamienił wskazanie na adres etykiety w pamięci
Przykłady:
Wypisanie liczby 10 na wyjście
| |
Dodawanie
| |
Adresowanie bezpośrednie
| |
Adresowanie pośrednie
| |
Pętla
| |
Ćwiczenia
dodac dwie liczby znajdujące się w pamięci
| |
- wypisac liczby znajdujące się w pamięci az napotkamy 0:
| |
- zsumować liczby znajdujące się w pamięci, zakończyć jak napotkamy 0:
| |
- wypisac na wyjście kolejne wartości ciągu fibonacciego, kilka pierwszych. Dla uproszczenia można dwie początkowe zapisać od razu w kodzie, np.:
| |
Symulator
| |
Analiza cyklu rozkazowego
Zdefiniowanie cyklu rozkazowego i jego faz (pobieranie, dekodowanie, wykonanie, dostęp do pamięci i zapis wyniku).
Cykl rozkazowy to sekwencja kroków, które wykonuje procesor w celu pobrania, zdekodowania i wykonania pojedynczego rozkazu. Cykl rozkazowy składa się z pięciu głównych faz, które są realizowane sekwencyjnie:
Pobieranie (Fetch): W tej fazie procesor pobiera rozkaz z pamięci. Wartość licznika rozkazów (Program Counter, PC) wskazuje na adres pamięci, z którego rozkaz ma być pobrany. Po pobraniu rozkazu, licznik rozkazów jest zwiększany o rozmiar rozkazu, aby wskazać na kolejny rozkaz.
Dekodowanie (Decode): Pobrany rozkaz jest dekodowany przez jednostkę dekodującą procesora, która interpretuje go i ustala, jakie operacje należy wykonać oraz które rejestry i/lub wartości są używane jako argumenty.
Wykonanie (Execute): W tej fazie jednostka wykonawcza procesora przeprowadza operacje zdefiniowane przez rozkaz. Może to obejmować działania arytmetyczne, logiczne, przesunięcia bitowe lub inne operacje. Wynik tych operacji jest przechowywany w rejestrze tymczasowym.
Dostęp do pamięci (Memory Access): Jeśli rozkaz wymaga dostępu do pamięci, na przykład w celu odczytania lub zapisania wartości, w tej fazie procesor odczytuje dane z pamięci lub zapisuje je w odpowiednim miejscu.
Zapis wyniku (Write-back): W tej ostatniej fazie wynik operacji, przechowywany w rejestrze tymczasowym, jest zapisywany do odpowiedniego rejestru procesora lub do pamięci, jeśli jest to wymagane.
Przykład analizy cyklu rozkazowego:
Rozważmy prosty przykład dodawania dwóch liczb, przechowywanych w rejestrach R1 i R2, a wynik ma być zapisany w rejestrze R3. Rozkaz może wyglądać tak: ADD R3, R1, R2
- Pobieranie: Procesor pobiera rozkaz ADD z adresu wskazanego przez licznik rozkazów (PC) i zwiększa wartość PC.
- Dekodowanie: Jednostka dekodująca interpretuje rozkaz jako operację dodawania, gdzie R1 i R2 są argumentami, a wynik ma być zapisany w R3.
- Wykonanie: Jednostka wykonawcza dodaje wartości z rejestru R1 i R2, a wynik przechowuje w rejestrze tymczasowym.
- Dostęp do pamięci: W tym przypadku nie ma potrzeby dostępu do pamięci, ponieważ wszystkie wartości są przechowywane w rejestrach.
- Zapis wyniku: Wynik dodawania, przechowywany w rejestrze tymczasow
Etapy cyklu rozkazowego.
Przyjmijmy prosty zestaw rozkazów oparty na hipotetycznym procesorze z ograniczoną architekturą. Rozkazy:
- LOAD R1, (ADDR) - Ładuje wartość z pamięci o adresie ADDR do rejestru R1.
- STORE (ADDR), R1 - Zapisuje wartość z rejestru R1 do pamięci o adresie ADDR.
- ADD R1, R2 - Dodaje wartości z rejestru R1 i R2, a wynik zapisuje w rejestrze R1.
- SUB R1, R2 - Odejmuje wartość rejestru R2 od wartości rejestru R1, a wynik zapisuje w rejestrze R1.
- JUMP ADDR - Bezwarunkowy skok do adresu ADDR.
- JNZERO R1, ADDR - Skok warunkowy do względnego adresu ADDR, jeśli wartość w rejestrze R1 jest różna od 0.
Omówienie poszczególnych etapów cyklu rozkazowego dla każdego z rozkazów:
LOAD R1, (ADDR):
- Pobieranie: Procesor pobiera rozkaz LOAD z pamięci.
- Dekodowanie: Dekodowanie rozkazu LOAD i identyfikacja rejestru R1 oraz adresu pamięci ADDR.
- Wykonanie: Brak operacji wykonawczych dla tego rozkazu.
- Dostęp do pamięci: Odczyt wartości z pamięci o adresie ADDR.
- Zapis wyniku: Zapisanie odczytanej wartości do rejestru R1.
STORE (ADDR), R1:
- Pobieranie: Procesor pobiera rozkaz STORE z pamięci.
- Dekodowanie: Dekodowanie rozkazu STORE i identyfikacja rejestru R1 oraz adresu pamięci ADDR.
- Wykonanie: Brak operacji wykonawczych dla tego rozkazu.
- Dostęp do pamięci: Zapis wartości z rejestru R1 do pamięci o adresie ADDR.
- Zapis wyniku: Brak operacji zapisu wyniku, ponieważ wynik został już zapisany w pamięci.
ADD R1, R2:
- Pobieranie: Procesor pobiera rozkaz ADD z pamięci.
- Dekodowanie: Dekodowanie rozkazu ADD i identyfikacja rejestrów R1 i R2.
- Wykonanie: Dodawanie wartości z rejestru R1 i R2, a wynik przechowuje w rejestrze tymczasowym.
- Dostęp do pamięci: Brak dostępu do pamięci, ponieważ wszystkie wartości są przechowywane w rejestrach.
- Zapis wyniku: Zapisanie wyniku dodawania do rejestru R1.
SUB R1, R2:
- Pobieranie: Procesor pobiera rozkaz SUB z pamięci.
- Dekodowanie: Dekodowanie rozkazu SUB i identyfikacja rejestrów R1 i R2.
- Wykonanie: Odejmowanie wartości rejestru R2 od wartości rejestru R1, a wynik przechowuje w rejestrze tymczasowym.
- Dostęp do pamięci: Brak dostępu do pamięci, ponieważ wszystkie wartości są przechowywane w rejestrach.
- Zapis wyniku: Zapisanie wyniku odejmowania do rejestru R1.
JUMP ADDR:
- Pobieranie: Procesor pobiera rozkaz JUMP z pamięci.
- Dekodowanie: Dekodowanie rozkazu JUMP i identyfikacja adresu ADDR.
- Wykonanie: Aktualizacja licznika rozkazów (PC) na wartość ADDR.
- Dostęp do pamięci: Brak dostępu do pamięci.
- Zapis wyniku: Brak operacji zapisu wyniku, ponieważ wynik został już zaktualizowany w liczniku rozkazów (PC).
JNZERO R1, ADDR:
- Pobieranie: Procesor pobiera rozkaz JZERO z pamięci.
- Dekodowanie: Dekodowanie rozkazu JZERO i identyfikacja rejestru R1 oraz adresu ADDR.
- Wykonanie: Sprawdzenie, czy wartość w rejestrze R1 wynosi 0.
- Dostęp do pamięci: Brak dostępu do pamięci.
- Zapis wyniku: Jeśli wartość w rejestrze R1 wynosi 0, aktualizacja licznika rozkazów (PC) o wartość ADDR. W przeciwnym razie PC zostaje zwiększone do kolejnego rozkazu.
Dla każdego z tych rozkazów analiza cyklu rozkazowego obejmuje omówienie poszczególnych faz (pobieranie, dekodowanie, wykonanie, dostęp do pamięci i zapis wyniku) oraz zrozumienie, jak procesor wykonuje te rozkazy sekwencyjnie. W przypadku procesorów z potokiem rozkazowym, kolejne rozkazy mogą być przetwarzane równocześnie w różnych fazach, zwiększając przepustowość procesora i efektywnie przyspieszając wykonywanie programu.
Prosty symulator cyklu rozkazowego
Lab_06:
Ćwiczenie:
- Proszę uruchomić pierwszy program: Lab_06_a
- Proszę opisać kolejne cykle rozkazowe, jakie wykonuje procesor
| |
- Proszę uruchomić drugi program: Lab_06_b
| |
- Proszę opisać cykle rozkazowe dla ostatniej instrukcji.
- Jakie jest działa drugi program? Proszę opisać.
Analiza potoku rozkazowego:
Potok rozkazowego i jego cele (zwiększenie przepustowości, równoległe wykonanie rozkazów).
Potok rozkazowy (ang. instruction pipeline) to technika wykorzystywana w mikroarchitekturze procesorów, mająca na celu zwiększenie przepustowości i wydajności przez równoczesne wykonywanie kilku rozkazów w różnych etapach ich przetwarzania. Potok rozkazowy dzieli cykl rozkazowy na kilka etapów, z których każdy może być przetwarzany równocześnie przez różne jednostki wykonawcze procesora. Dzięki temu, zamiast czekać na zakończenie jednego rozkazu, procesor może przetwarzać kolejne rozkazy, zwiększając przepustowość i efektywnie przyspieszając wykonywanie programu.
Cele potoku rozkazowego:
Zwiększenie przepustowości: Potok rozkazowy pozwala na równoczesne przetwarzanie kilku rozkazów w różnych etapach cyklu rozkazowego, co zwiększa przepustowość procesora i pozwala na szybsze wykonanie programu.
Równoległe wykonanie rozkazów: Potok rozkazowy pozwala na równoczesne wykonywanie różnych operacji w różnych jednostkach wykonawczych procesora, co oznacza, że procesor może jednocześnie wykonywać operacje na różnych danych, zwiększając wydajność obliczeń.
Przykład potoku rozkazowego
Załóżmy, że mamy prosty procesor z czterema etapami cyklu rozkazowego: pobieranie (IF - Instruction Fetch), dekodowanie (ID - Instruction Decode), wykonanie (EX - Execute) i zapis wyniku (WB - Write Back). Potok rozkazowy dla tego procesora będzie miał cztery etapy, które można wykonać równocześnie dla różnych rozkazów.
| |
Jak widać na powyższym przykładzie, potok rozkazowy pozwala na równoczesne przetwarzanie kilku rozkazów w różnych etapach cyklu rozkazowego. W momencie, gdy pierwszy rozkaz jest w fazie wykonania (EX), drugi rozkaz jest w fazie dekodowania (ID), a trzeci rozkaz jest pobierany (IF). Dzięki temu procesor może jednocześnie pracować nad różnymi rozkazami, zwiększając swoją przepustowość i wydajność.
Jednakże, potok rozkazowy wprowadza również pewne wyzwania, takie jak zarządzanie hazardami (ang. hazards). Hazardy to sytuacje, w których wynik jednego rozkazu jest potrzebny przez następny rozkaz, a potok rozkazowy musi zarządzać tymi zależnościami, aby uniknąć konflikty lub zależności.
Istnieją trzy główne rodzaje hazardów:
Hazardy strukturalne: Występują, gdy różne rozkazy próbują jednocześnie korzystać z tego samego zasobu procesora, takiego jak jednostka wykonawcza, pamięć czy rejestry. Hazardy strukturalne mogą prowadzić do opóźnień lub konieczności oczekiwania przez niektóre rozkazy na dostęp do zasobów.
Sposoby minimalizowania hazardów strukturalnych:
- Wprowadzenie dodatkowych zasobów: Zwiększenie liczby jednostek wykonawczych, pamięci czy rejestrów może zmniejszyć ryzyko wystąpienia konfliktów.
- Replikacja zasobów: Dodatkowe zasoby pozwalają na równoczesne korzystanie z nich przez różne rozkazy.
- Wykorzystanie buforów i kolejkowania: Buforowanie i kolejkowanie operacji może pomóc w zarządzaniu dostępem do zasobów i zmniejszyć opóźnienia.
Hazardy danych: Występują, gdy jeden rozkaz jest zależny od wyniku innego rozkazu, który jeszcze nie został zakończony. Hazardy danych mogą prowadzić do nieprawidłowych wyników, jeśli nie zostaną odpowiednio obsłużone.
Sposoby minimalizowania hazardów danych:
- Przesunięcie potoku (stalling): Wstrzymywanie wykonywania zależnego rozkazu aż do momentu, gdy wynik potrzebny dla tego rozkazu będzie dostępny.
- Przekształcanie potoku (forwarding): Przekazanie wyniku zależnego rozkazu bezpośrednio do kolejnego rozkazu, bez konieczności zapisywania wyniku w rejestrze.
- Przeplanowanie rozkazów: Kompilator lub procesor może próbować zmienić kolejność rozkazów, aby zmniejszyć zależności i poprawić wydajność potoku rozkazowego.
Hazardy kontroli: Występują, gdy kolejność wykonywania rozkazów ulega zmianie z powodu instrukcji warunkowych, takich jak skoki czy instrukcje warunkowe. Hazardy kontroli mogą prowadzić do niepotrzebnego wypełnienia potoku rozkazów i straty wydajności.
Ref:
Sposoby minimalizowania hazardów kontroli:
- Przewidywanie rozgałęzień (branch prediction): Procesor próbuje przewidywać, czy dane rozgałęzienie zostanie wykonane, i wstępnie ładuje odpowiednie rozkazy do potoku rozkazowego.
- Opóźnianie rozgałęzienia (branch delay slot): Procesor pozwala na wykonanie jednego lub kilku rozkazów po instrukcji rozgałęzienia, zanim rzeczywista zmiana przepływu sterowania zostanie wprowadzona. Kompilator może umieścić niezależne rozkazy w tych opóźnionych miejscach, aby zmniejszyć straty wydajności spowodowane hazardami kontroli.
- Wykonanie spekulatywne (speculative execution): Procesor wykonuje obie ścieżki po rozgałęzieniu warunkowym, jednocześnie śledząc poprawność wyników. Gdy warunek rozgałęzienia zostanie ostatecznie wyznaczony, procesor odrzuca wyniki niewłaściwej ścieżki i kontynuuje wykonanie poprawnej ścieżki.
Ref: Interesująca podatność związana z SE (side-channel) - Spectre - wiki Spectre Attacks: Exploiting Speculative Execution Meltdown Security Vulnerability Meltdown Proof-of-Concept
Podatność Spectre dotyczy złośliwego wykorzystania spekulatywnego wykonania instrukcji przez procesor w celu uzyskania dostępu do poufnych informacji.
Przetwarzanie wielowątkowe (multithreading): Procesor może przełączać się między różnymi wątkami wykonawczymi, gdy napotyka hazardy kontroli. Pozwala to na utrzymanie potoku rozkazowego aktywnym i wydajnym, nawet gdy jeden wątek oczekuje na wynik rozgałęzienia.
W praktyce zaawansowane mikroarchitektury procesorów stosują różne techniki, aby zarządzać hazardami potoku rozkazowego i zwiększać wydajność procesora. Optymalizacja wykorzystania potoku rozkazowego, zarządzanie hazardami oraz przyspieszenie wykonywania programów są kluczowe dla osiągnięcia wysokiej wydajności w nowoczesnych procesorach.
Przykładowe sposoby minimalizacji hazardów
- Hazard strukturalny: Załóżmy, że mamy procesor z jednym modułem ALU (Arithmetic Logic Unit) i poniższymi rozkazami do wykonania:
| |
Wszystkie trzy rozkazy wymagają dostępu do ALU. W celu zapobieżenia hazardom strukturalnym, procesor może:
Wprowadzić dodatkowe moduły ALU, aby umożliwić równoczesne wykonywanie różnych operacji.
Zastosować buforowanie i kolejkowanie operacji, aby zarządzać dostępem do ALU i zmniejszyć opóźnienia.
Hazard danych: Załóżmy, że mamy następujący ciąg rozkazów:
| |
Wynik rozkazu 1 (ADD) jest używany jako wejście dla rozkazu 2 (SUB), a wynik rozkazu 2 jest używany jako wejście dla rozkazu 3 (MUL). W celu zarządzania hazardami danych, procesor może:
Wstrzymać wykonywanie rozkazu 2 (stalling), aż do momentu, gdy wynik rozkazu 1 będzie dostępny.
Zastosować przekształcanie potoku (forwarding), przekazując wynik rozkazu 1 bezpośrednio do rozkazu 2, bez konieczności zapisywania wyniku w rejestrze.
Hazard kontroli: Załóżmy, że mamy następujący ciąg rozkazów z instrukcją warunkowego skoku:
| |
W przypadku hazardu kontroli spowodowanego przez instrukcję warunkowego skoku (JNE), procesor może:
- Zastosować przewidywanie rozgałęzień (branch prediction), próbując przewidzieć, czy skok zostanie wykonany, i wstępnie ładując odpowiednie rozkazy do potoku rozkazowego.
- Wykorzystać opóźnienie rozgałęzienia (branch delay slot), umieszczając jeden lub więcej niezależnych rozkazów po instrukcji skoku, które zostaną wykonane przed rzeczywistym skokiem
W praktyce, zaawansowane mikroarchitektury procesorów stosują różne techniki, aby zarządzać hazardami potoku rozkazowego i zwiększać wydajność procesora, takie jak przewidywanie rozgałęzień, optymalizacja wykonywania potoku czy wykorzystanie wielowątkowości.
Zadanie z symulacją: symulator potoku rozkazowego dla prostego procesora, uwzględniając hazardy.
Hazard danych
Prosty procesor z potokiem rozkazowym o 4 etapach (IF - pobieranie rozkazu, ID - dekodowanie, EX - wykonanie, WB - zapis wyniku)
Lab_07
Powyższy symulator wykonuje sekwencję rozkazów (program) na prostym procesorze. Wprowadza wstrzymanie (stalling) potoku, gdy wykryje hazard danych, co pozwala na zaktualizowanie wartości rejestru przed przekazaniem go do kolejnego rozkazu. Symulator wyświetla etap potoku dla każdego rozkazu oraz numer cyklu. Po zakończeniu symulacji wyświetlane są końcowe wartości rejestrów procesora.
Hazard kontroli
Symulator prostego procesora z uwzględnieniem hazardu kontroli (branch hazard). Procesor ten ma prosty potok rozkazów o pięciu etapach: pobieranie rozkazu (IF), dekodowanie (ID), wykonanie (EX), dostęp do pamięci (MEM) i zapis wyniku (WB).
Lab_07 + branch predictor
Symulator wykonuje sekwencję rozkazów na prostym procesorze z potokiem rozkazowym. Wprowadza wstrzymanie (stalling) potoku, gdy wykryje hazard kontroli (branch hazard), co pozwala na zaktualizowanie wartości PC przed pobraniem kolejnego rozkazu. Symulator wyświetla etap potoku dla każdego rozkazu oraz numer cyklu. Po zakończeniu symulacji wyświetlane są końcowe wartości rejestrów procesora.
Instruction reordering
Uwaga: Warto zauważyć, że efekty takie jak reordering instrukcji są zależne od architektury procesora, a w przypadku niektórych implementacji może być trudno uzyskać te efekty w sposób powtarzalny.
Oto prosty program w C++, który ilustruje reordering instrukcji na procesorze x86:
Lab_10
| |
W tym programie używamy dwóch zmiennych atomowych x i y, które są inicjowane wartością 0. Wątek t1 zapisuje wartość 1 do x i y, podczas gdy wątek t2 wczytuje wartości y i x. Używamy relaksowanej kolejności pamięci (std::memory_order_relaxed), która pozwala na reordering instrukcji.
Jeśli procesor przestawi kolejność instrukcji w taki sposób, że odczyt y zostanie wykonany przed odczytem x, program zlicza taką sytuację jako reordering.
Po wielokrotnym uruchomieniu programu liczba reorderingów może być różna. Procesor x86 ma silną kolejność pamięci, więc reordering instrukcji może być rzadko spotykany. Przetestuj ten program na różnych konfiguracjach sprzętowych, aby zobaczyć, jak efekty reorderingu instrukcji różnią się w zależności od sprzętu.
Ref:
Porównanie jedno- i wielordzeniowych procesorów:
Różnice
Jednordzeniowe i wielordzeniowe procesory to dwa różne typy układów scalonych stosowanych w komputerach. Definicje, zalety i wady każdego z nich.
Jednordzeniowy procesor (single-core processor)
Definicja: Procesor jednordzeniowy to układ scalony z jednym rdzeniem CPU, który może wykonywać tylko jedną instrukcję na raz.
Zalety:
- Mniejsza złożoność układu: Jednordzeniowe procesory są mniej skomplikowane w porównaniu do wielordzeniowych, co może prowadzić do mniejszego zużycia energii i niższych kosztów produkcji.
- Łatwiejsza implementacja: Programowanie dla jednordzeniowych procesorów jest prostsze, ponieważ nie ma konieczności zarządzania równoczesnością.
Wady:
- Niska wydajność: W przypadku zadań wielowątkowych, jednordzeniowe procesory mają niższą wydajność niż ich wielordzeniowe odpowiedniki, ponieważ mogą wykonywać tylko jedno zadanie na raz.
- Szybsze osiąganie limitów wydajności: Ponieważ jednordzeniowe procesory mają tylko jeden rdzeń, mogą szybciej osiągnąć swoje limity wydajności, co prowadzi do niższej wydajności w porównaniu do wielordzeniowych procesorów.
Przykład w C++:
Lab_11
| |
Wielordzeniowy procesor (multi-core processor)
Definicja: Wielordzeniowy procesor to układ scalony z dwoma lub więcej rdzeniami CPU, które mogą równocześnie wykonywać wiele instrukcji.
Zalety:
- Wyższa wydajność: Wielordzeniowe procesory są bardziej wydajne dla zadań wielowątkowych, ponieważ mogą równocześnie wykonywać wiele zadań.
- Skalowalność: Wielordzeniowe procesory mogą być łatwiej skalowane, co prowadzi do wyższej wydajności w porównaniu do jednordzeniowych procesorów.
- Energooszczędność: W przypadku zastosowań o małym obciążeniu, wielordzeniowe procesory mogą oszczędzać energię poprzez wyłączanie nieużywanych rdzeni.
Wady:
- Wyższa złożoność układu: Wielordzeniowe procesory są bardziej skomplikowane niż jednordzeniowe, co może prowadzić do wyższego zużycia energii i wyższych kosztów produkcji.
- Trudniejsza implementacja: Programowanie dla wielordzeniowych procesorów może być trudniejsze, ponieważ wymaga zarządzania równoczesnością i synchronizacją między wątkami.
Przykład w C++:
Lab_12
| |
W powyższym przykładzie używamy biblioteki <thread> w języku C++ do tworzenia dwóch wątków, które wykonują funkcje add() i sub() równocześnie na wielordzeniowym procesorze. Dzięki temu można równocześnie obliczyć sumę i różnicę dwóch liczb, co pokazuje zaletę wielordzeniowego procesora w porównaniu do jednordzeniowego procesora.
Jednordzeniowe procesory są prostsze, ale mniej wydajne, szczególnie w przypadku zadań wielowątkowych. Wielordzeniowe procesory oferują wyższą wydajność dla zadań wielowątkowych, ale wymagają bardziej zaawansowanego zarządzania równoczesnością i synchronizacją w kodzie programu. Wybór pomiędzy nimi zależy od konkretnych wymagań i ograniczeń projektu.
UWAGA: Problem wyścigu (race condition)
Ref:
Hyper-threading
Hyper-threading to technologia opracowana przez firmę Intel, która pozwala na wykonywanie dwóch lub więcej wątków na jednym rdzeniu procesora, zwiększając wydajność procesora w zadaniach wielowątkowych. Technologia ta polega na tym, że jeden rdzeń procesora posiada dwa lub więcej zestawów rejestrów, które są niezależne dla każdego wątku. Dzięki temu rdzeń może wykonywać wiele wątków równocześnie, wykorzystując jednocześnie swoje zasoby sprzętowe.
W uproszczonym procesorze z technologią Hyper-threading można uwzględnić następujące elementy:
Rdzeń procesora: Jednostka wykonawcza (ALU), jednostka sterująca oraz pamięć podręczna (cache). Rdzeń procesora wykonuje instrukcje z kolejnych wątków.
Zestawy rejestrów: Każdy wątek posiada swój własny zestaw rejestrów, takich jak licznik programu (PC) oraz rejestry ogólnego przeznaczenia. W przypadku procesora z technologią Hyper-threading, rdzeń posiada dwa lub więcej zestawów rejestrów, które są niezależne dla każdego wątku.
Mechanizm przemiennego wykonania instrukcji (Instruction interleaving): Procesor z technologią Hyper-threading wykonuje instrukcje z różnych wątków w sposób przemienny. Gdy jeden wątek jest zablokowany, np. na wynik operacji I/O, procesor może kontynuować wykonywanie instrukcji z innego wątku, dzięki czemu zasoby sprzętowe rdzenia są lepiej wykorzystane.
Mechanizm równoczesnego dekodowania (Simultaneous multithreading, SMT): Procesor z technologią Hyper-threading może równocześnie dekodować i wykonywać instrukcje z różnych wątków, co przyczynia się do zwiększenia wydajności procesora w zadaniach wielowątkowych.
Mechanizm zarządzania wątkami: Procesor z technologią Hyper-threading posiada mechanizm zarządzania wątkami, który kontroluje ich wykonanie, przydzielanie zasobów oraz obsługę zdarzeń, takich jak przerwania czy wyjątki.
Podsumowując, technologia Hyper-threading pozwala na efektywne wykorzystanie zasobów sprzętowych rdzenia procesora, zwiększając jego wydajność w zadaniach wielowątkowych. W procesorze z technologią Hyper-threading znajduje się rdzeń, który posiada dwa lub więcej niezależnych zestawów rejestrów, umożliwiających równoczesne wykonywanie instrukcji z różnych wątków. Procesor z Hyper-threading posiada także mechanizmy takie jak Instruction interleaving, Simultaneous multithreading (SMT) oraz zarządzanie wątkami, które kontrolują wykonanie, przydzielanie zasobów oraz obsługę zdarzeń.
Oto kilka zalet i wad technologii Hyper-threading:
Zalety:
- Zwiększona wydajność: Technologia Hyper-threading pozwala na lepsze wykorzystanie zasobów rdzenia procesora, co prowadzi do zwiększenia wydajności w zadaniach wielowątkowych.
- Lepsza przepustowość: Dzięki możliwości równoczesnego wykonywania instrukcji z różnych wątków, procesor z technologią Hyper-threading może osiągnąć wyższą przepustowość w porównaniu do procesora bez tej technologii.
- Efektywność energetyczna: Procesory z technologią Hyper-threading mogą wykorzystywać swoje zasoby sprzętowe efektywniej, co może prowadzić do oszczędności energii.
Wady:
- Zwiększona złożoność: Technologia Hyper-threading wprowadza dodatkową złożoność w architekturze procesora, co może prowadzić do wyższych kosztów produkcji i trudności w debugowaniu.
- Potencjalne problemy z synchronizacją: W przypadku równoczesnego wykonywania wielu wątków na jednym rdzeniu, mogą wystąpić problemy z synchronizacją oraz konkurencją o zasoby sprzętowe.
- Wydajność w zależności od rodzaju zadania: Technologia Hyper-threading przynosi korzyści głównie w zadaniach wielowątkowych, a jej wpływ na wydajność w zadaniach jednowątkowych może być ograniczony.
Warto zauważyć, że technologia Hyper-threading nie jest jedyną dostępną techniką SMT (Simultaneous multithreading) - inne firmy, takie jak AMD, opracowały własne technologie SMT, takie jak SMT w procesorach AMD Ryzen, które oferują podobne możliwości wykonywania wielu wątków na jednym rdzeniu procesora. W zastosowaniach praktycznych, wybór procesora z technologią Hyper-threading czy innymi technologiami SMT zależy od potrzeb konkretnego projektu oraz rodzaju zadań, które mają być realizowane.
Diagram procesora z technologią Hyper-threading:
| |
Symulacja działania procesora z HT
Lab_13
| |
W powyższym kodzie, klasa Processor symuluje prosty procesor z technologią Hyper-threading. Ma jeden rdzeń, który może wykonywać operacje dodawania. Rejestry są podzielone na dwa zestawy, po jednym dla każdego wątku. W funkcji execute, procesor dekoduje i wykonuje operacje na podstawie identyfikatora wątku.
W funkcji main, tworzymy dwa wątki, które wykonują operacje dodawania równocześnie. Dzięki temu symulator ilustruje, jak procesor z technologią Hyper-threading może wykonywać wiele wątków na jednym rdzeniu procesora.
Scenariusz problemu i porównanie rozwiązania na procesorze jedno- i wielordzeniowym.
Komunikacja z pamięcią - odczyt
Ref:
Rodzaje
Pamięć podręczna procesora: Jest to niewielka ilość pamięci wbudowana w jednostkę centralną komputera (CPU), która przechowuje często używane dane i instrukcje. Pamięć podręczna CPU przyspiesza procesorowi dostęp do danych i instrukcji, dzięki czemu nie musi on tak często sięgać do wolniejszej pamięci głównej lub urządzeń pamięci masowej.
Pamięć podręczna: Jest to niewielka część pamięci głównej (RAM) odłożona jako tymczasowy obszar przechowywania często używanych danych. Buforowanie pamięci pomaga poprawić wydajność aplikacji poprzez skrócenie czasu dostępu do danych z wolniejszych nośników pamięci, takich jak dyski twarde lub sieci.
Pamięć podręczna dysku: Jest to część pamięci głównej (RAM) używana do przechowywania danych, które zostały niedawno odczytane lub zapisane na dysku, takim jak dysk twardy lub dysk półprzewodnikowy. Buforowanie dysku pomaga zmniejszyć liczbę operacji odczytu i zapisu na dysku, poprawiając ogólną wydajność systemu. Pamięć podręczna przeglądarki: Jest to tymczasowy obszar przechowywania treści internetowych, takich jak strony HTML, obrazy i inne media, które są przechowywane w pamięci podręcznej przeglądarki internetowej. Gdy użytkownik odwiedza stronę internetową, jego przeglądarka przechowuje kopię zawartości strony w pamięci podręcznej. Gdy użytkownik ponownie odwiedza tę samą stronę internetową, przeglądarka może załadować zawartość z pamięci podręcznej zamiast pobierać ją ponownie, co może skrócić czas ładowania strony.
Rozproszona pamięć podręczna: Jest to pamięć podręczna, która jest współdzielona przez wiele komputerów w sieci i służy do przechowywania często używanych danych, które są rozproszone na wielu serwerach. Zmniejszając potrzebę dostępu do danych z wielu serwerów, rozproszone buforowanie może poprawić wydajność systemów rozproszonych. Rozproszone buforowanie może również poprawić skalowalność aplikacji, ponieważ dane mogą być buforowane w wielu lokalizacjach, co oznacza, że więcej jednoczesnych użytkowników może uzyskać dostęp do danych przy mniejszej liczbie żądań
Czym jest pamięć podręczna (w procesorze)?
Pamięć podręczna (ang. cache memory) to typ pamięci w komputerze, który przechowuje dane, do których komputer często się odwołuje. W przeciwieństwie do głównej pamięci komputera (RAM), pamięć podręczna jest zazwyczaj znacznie szybsza, ale ma też znacznie mniejszą pojemność.
Podstawowym celem pamięci podręcznej jest zwiększenie efektywności działania komputera. Gdy komputer potrzebuje danych, najpierw sprawdza, czy są one przechowywane w pamięci podręcznej. Jeżeli tak, dane są ładowane stamtąd, co jest szybsze niż ładowanie ich z pamięci RAM lub dysku twardego. Jeżeli danych nie ma w pamięci podręcznej, są one ładowane z innej pamięci i jednocześnie umieszczane w pamięci podręcznej, aby były dostępne na przyszłość.
Pamięć podręczna jest organizowana na kilka poziomów (L1, L2, L3, itd.), gdzie L1 jest najbliżej procesora (i zazwyczaj najszybsza, ale też najmniejsza), a kolejne poziomy są coraz dalej (i zazwyczaj coraz wolniejsze, ale większe).
Diagramy, które pokazują, jak działa pamięć podręczna, mogą być różne w zależności od szczegółów implementacji i architektury. Poniżej znajduje się proste wyjaśnienie na przykładzie trzech poziomów pamięci podręcznej (L1, L2, L3):
| |
Pentium M
| To Where | Cycles |
|---|---|
| Register | ≤ 1 |
| L1d | ∼ 3 |
| L2 | ∼ 14 |
| Main Memory | ∼ 240 |
Drepper, (what every programmer should know…)
Pobieranie danych do pamięci podręcznej
Dane są pobierane do pamięci podręcznej przez proces zwanym polityką pamięci podręcznej (ang. cache policy). Istnieją różne strategie zarządzania pamięcią podręczną, ale dwie najpopularniejsze to:
LRU (Least Recently Used): W tej strategii, gdy pamięć podręczna jest pełna i trzeba dodać nowe dane, usuwany jest element, który nie był używany przez najdłuższy czas. Idea jest taka, że jeśli dane nie były używane od dawna, prawdopodobnie nie będą potrzebne w najbliższej przyszłości.
LFU (Least Frequently Used): W tej strategii, gdy pamięć podręczna jest pełna i trzeba dodać nowe dane, usuwany jest element, który był używany najrzadziej. Ta strategia zakłada, że jeśli dane były rzadko używane w przeszłości, prawdopodobnie nie będą często używane w przyszłości.
Gdy komputer potrzebuje danych, najpierw sprawdza, czy są one przechowywane w pamięci podręcznej. Jeżeli tak, dane są ładowane stamtąd, co jest znacznie szybsze niż ładowanie ich z pamięci RAM lub dysku twardego. To jest nazywane “trafieniem” (ang. cache hit). Jeżeli danych nie ma w pamięci podręcznej, to jest nazywane “pudłem” (ang. cache miss) i dane są ładowane z wolniejszego źródła (np. pamięci RAM lub dysku twardego), a następnie umieszczane w pamięci podręcznej, aby były dostępne na przyszłość.
W przypadku pudła, dane mogą być ładowane do pamięci podręcznej na dwa główne sposoby:
Polityka pobierania przy pudle (ang. fetch on miss): Gdy dane nie są w pamięci podręcznej, są one pobierane z wolniejszego źródła i umieszczane w pamięci podręcznej.
Polityka pobierania z wyprzedzeniem (ang. prefetch): W tej strategii, komputer próbuje przewidzieć, jakie dane będą potrzebne w przyszłości i ładować je do pamięci podręcznej z wyprzedzeniem, zanim będą rzeczywiście potrzebne.
Oczywiście, te strategie są uproszczeniami, a rzeczywiste systemy pamięci podręcznej mogą korzystać z bardziej skomplikowanych algorytmów i strategii, które biorą pod uwagę wiele czynników, takich jak lokalność odwołań do danych (tj. tendencja do odwoływania się do tych samych danych wielokrotnie w krótkim okresie czasu) czy hierarchię pamięci podręcznej.
Nomenklatura
Level 1 data cache - 48 kB, 12 way, 64 sets, 64 B line size, latency 5, per core
48 kB: The size of the L1 data cache is 48 kilobytes. This is the total amount of data that can be stored in the cache. Smaller caches are faster but can store less data, while larger caches can store more data but may be slower.
12 way: This refers to the cache’s associativity, which determines how cache lines can be mapped to cache sets. In a 12-way associative cache, each cache set can hold 12 different cache lines. Higher associativity can reduce the likelihood of cache conflicts (when multiple cache lines map to the same cache set), but may increase access latency.
64 sets: The cache is divided into 64 sets. Each set can store multiple cache lines, as determined by the cache’s associativity (in this case, 12-way).
64 B line size: The size of each cache line is 64 bytes. When data is fetched from the main memory, it is brought into the cache in blocks called cache lines. A larger cache line size can improve spatial locality (the likelihood that nearby memory locations will be accessed), but may also result in more unused data being fetched.
Latency 5: The cache latency is 5 clock cycles. This is the time it takes for the processor to access data stored in the L1 cache.
Per core: This specification is for an L1 data cache that is dedicated to each core in a multicore processor. Each core has its own L1 data cache, which can help improve performance by reducing contention for cache resources between cores.
Pamięć Wirtualna
Pamięć wirtualna to technika zarządzania pamięcią, która pozwala na wykorzystanie dysku twardego jako rozszerzenia pamięci fizycznej RAM. Dzięki temu programy mogą używać więcej pamięci, niż jest dostępna fizycznie w systemie.
System operacyjny przypisuje każdemu programowi obszar pamięci, który nazywany jest przestrzenią adresową. Każda przestrzeń adresowa jest podzielona na bloki o stałym rozmiarze, zwane stronami. W systemach z pamięcią wirtualną, nie wszystkie strony muszą być zawsze przechowywane w pamięci RAM. Kiedy program próbuje odwołać się do strony, która nie jest obecnie w pamięci, system operacyjny przenosi ją z dysku do RAM.
Pamięć wirtualna ma kilka zalet.
- Pozwala na uruchamianie programów, które wymagają więcej pamięci, niż jest dostępne.
- Poprawia bezpieczeństwo, ponieważ programy nie mają bezpośredniego dostępu do pamięci RAM, co utrudnia wykorzystanie błędów w programach do ataków na system.
Jednak pamięć wirtualna ma też swoje wady. Przede wszystkim, jest wolniejsza od pamięci RAM, ponieważ odczyt i zapis na dysk są wolniejsze niż operacje w pamięci. Po drugie, jeśli system operacyjny musi często przenosić strony pomiędzy RAM a dyskiem (co nazywa się “thrashing”), może to poważnie obniżyć wydajność systemu.
Mechanizmy potrzebne do implementacji pamięci wirtualnej:
Obsługa stronicowania pamięci (paging): Procesory muszą mieć mechanizm umożliwiający mapowanie przestrzeni adresowej na strony pamięci. W rzeczywistości to stronicowanie umożliwia obsługę pamięci wirtualnej - strony, które nie są obecnie potrzebne, mogą być przeniesione na dysk twardy, a następnie ponownie załadowane do pamięci RAM, gdy są potrzebne.
Mechanizm zarządzania pamięcią (MMU - Memory Management Unit): MMU to sprzętowy komponent procesora, który przetwarza i kontroluje wszystkie odwołania do pamięci. MMU jest odpowiedzialny za translację adresów wirtualnych na adresy fizyczne. Jest to kluczowe dla obsługi pamięci wirtualnej, ponieważ pozwala programom “myśleć”, że mają dostęp do ciągłego bloku pamięci, podczas gdy w rzeczywistości ich strony mogą być rozproszone w różnych miejscach pamięci fizycznej.
Mechanizmy ochrony pamięci: Procesory muszą mieć mechanizmy umożliwiające kontrolę dostępu do pamięci. Dzięki temu system operacyjny może zapobiegać sytuacjom, w których jeden proces próbuje odczytać lub zapisywać w obszarze pamięci innego procesu.
Mechanizmy obsługi przerwań: Kiedy program próbuje odwołać się do strony, która nie jest obecnie w pamięci, procesor generuje przerwanie (tzw. page fault), które jest obsługiwane przez system operacyjny. System operacyjny wtedy przenosi stronę z dysku do pamięci i kontynuuje wykonywanie programu.
Każda z tych cech jest kluczowa dla obsługi pamięci wirtualnej i jest obecna we współczesnych procesorach.
Lab_15
W poniższym programie przetestujemy dwa różne sposoby dostępu do pamięci: sekwencyjny i losowy. Porównamy czas wykonania obu podejść, które mogą wpływać na wykorzystanie pamięci cache.
Ćwiczenie: Proszę uruchomić program, opisać w sprawozdaniu jego wynik.
| |
Należy modyfikować ilość iteracji: 50 75 100, uruchamiając dla dostępu sekwencyjnego i losowego.
Ref:
W symulatorze mamy prostą pamięć cache, która przechowuje wartości z pamięci. Procesor korzysta z cache podczas sekwencyjnego i losowego dostępu do pamięci. Symulator mierzy czas dostępu do pamięci oraz liczbę trafień cache dla obu podejść.
Uruchomienie tego symulatora pokaże, że sekwencyjny dostęp do pamięci jest szybszy niż losowy, ponieważ lepiej wykorzystuje pamięć cache. Ponadto, liczba trafień cache jest większa dla sekwencyjnego dostępu do pamięci w porównaniu z losowym dostępem.
Zmiana parametrów symulatora (rozmiar pamięci, rozmiar cache, liczba iteracji) w celu zrozumienia, jak wpływają na wyniki.
Symulator pamięci podręcznej (cache) typu direct-mapped
Lab_17
Proszę uruchomić program, opisać w sprawozdaniu jego wynik. Należy kilka razy zmodyfikować parametry:
-c 1024 -b 32 -n 10000 -m 2048-c 1024 -b 64 -n 10000 -m 2048-c 2048 -b 32 -n 10000 -m 4096-c 2048 -b 64 -n 10000 -m 4096- inna konfiguracja wg uznania z taką samą liczbą iteracji
- inna konfiguracja wg uznania z taką samą liczbą iteracji
| |
Lab_18 Prefetch
Proszę uruchomić program, opisać w sprawozdaniu jego wynik. Należy kilka razy zmodyfikować parametry:
-c 1024 -b 32 -n 10000 -m 2048 -d 1-c 1024 -b 64 -n 10000 -m 2048 -d 2-c 2048 -b 32 -n 10000 -m 4096 -d 4-c 2048 -b 64 -n 10000 -m 4096 -d 8- inna konfiguracja wg uznania z taką samą liczbą iteracji
- inna konfiguracja wg uznania z taką samą liczbą iteracji
$lab_18.exe -c 1024 -b 32 -n 10000 -m 1024 -d 8
-c, –cache size -b, –block size -n, –iteration -m, –memory size -d, –prefetch distance
| |